Research

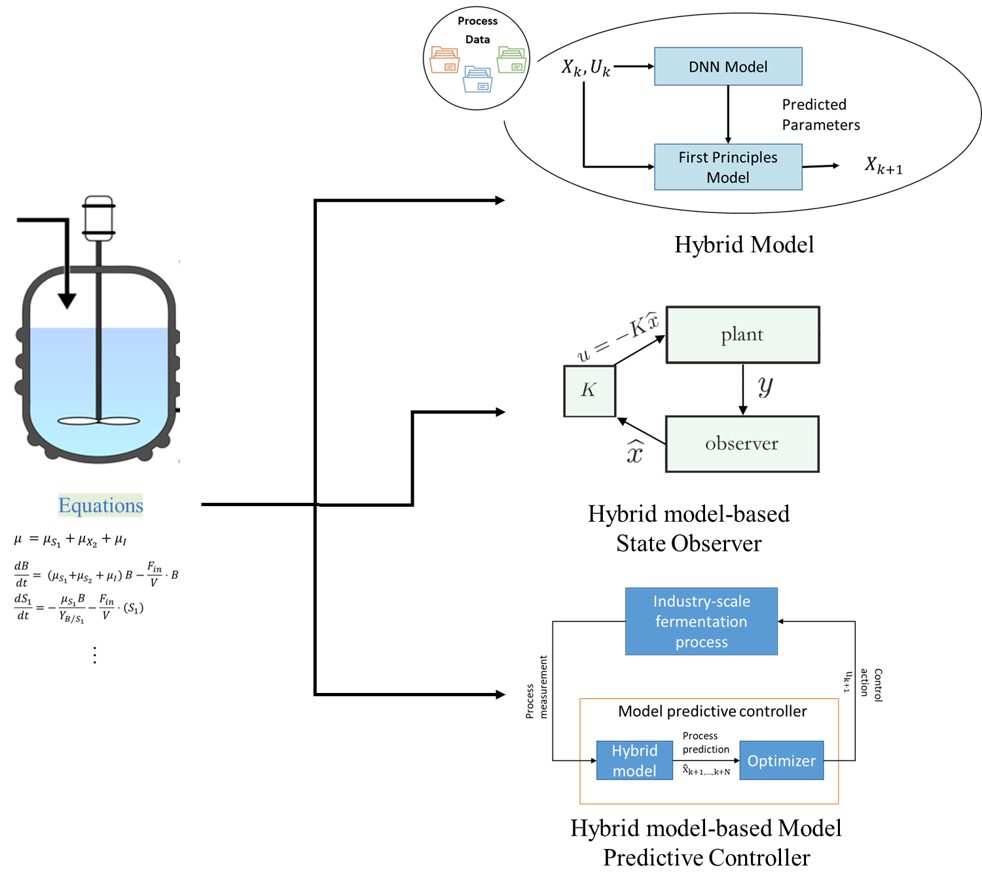
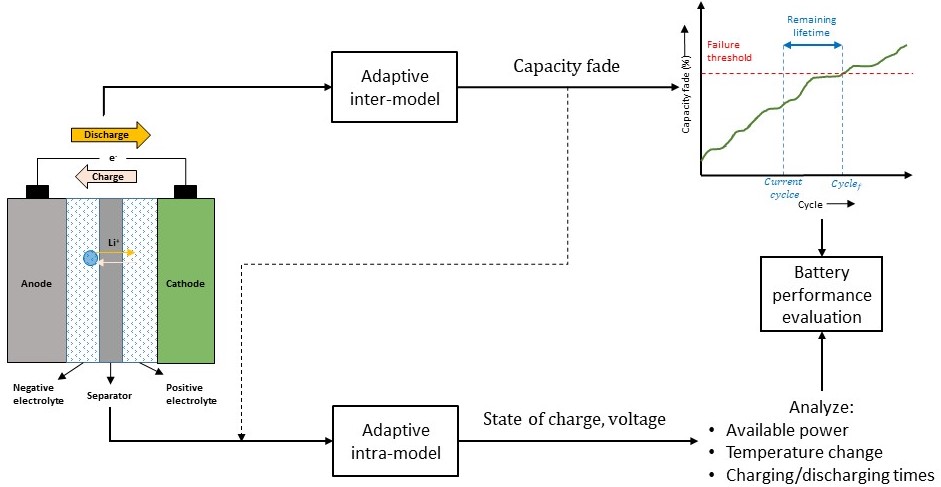
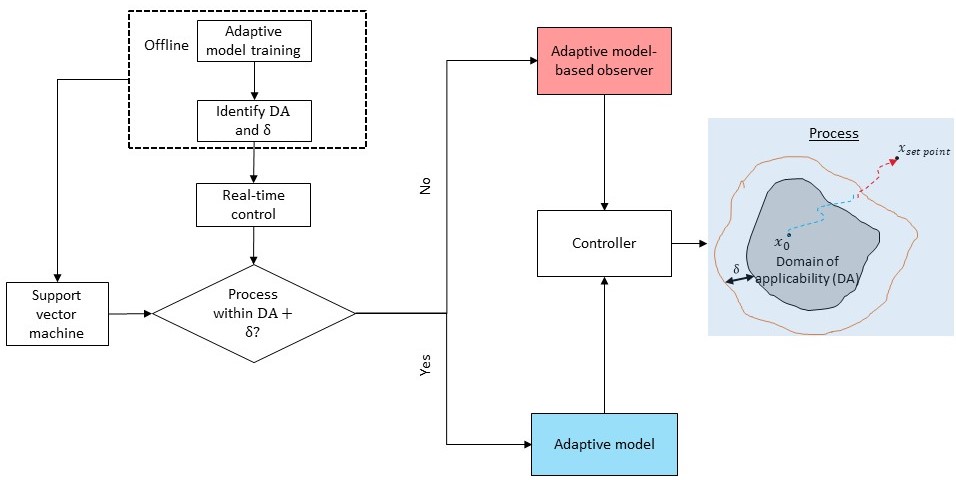
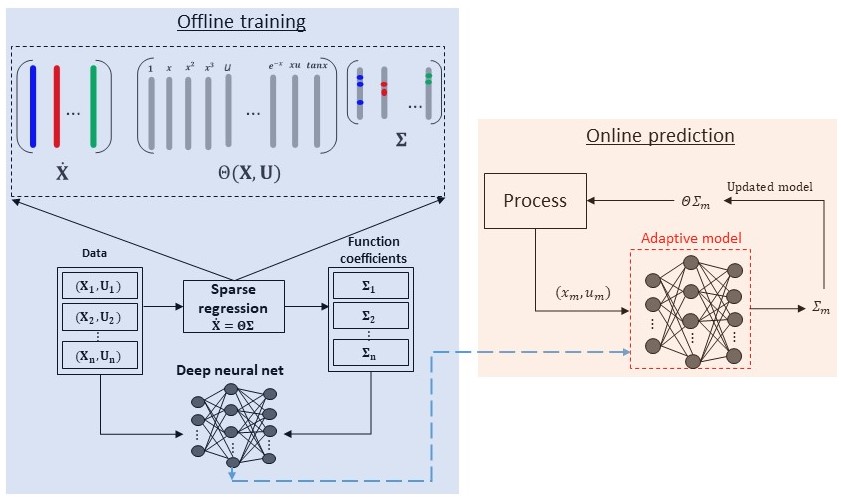
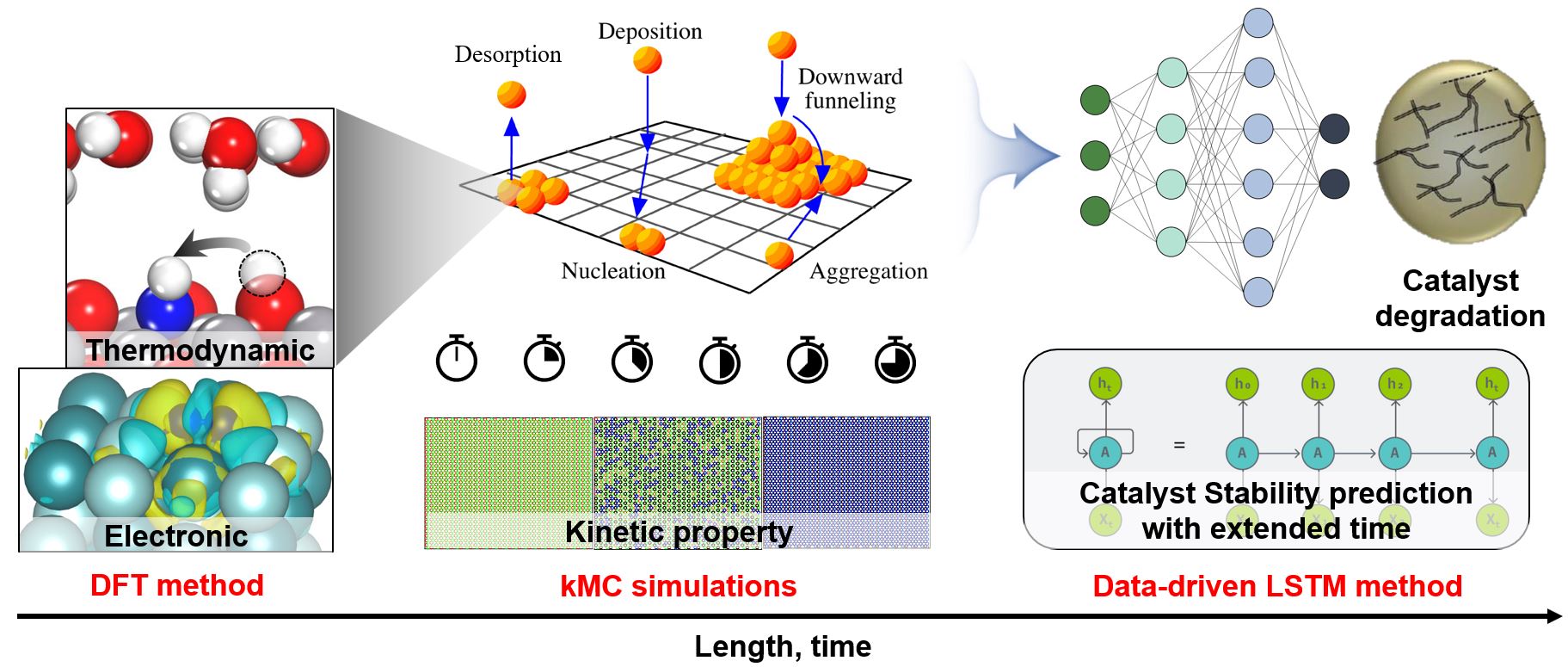
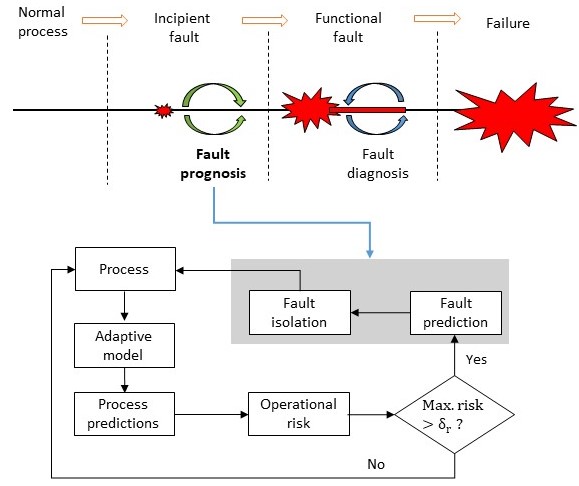
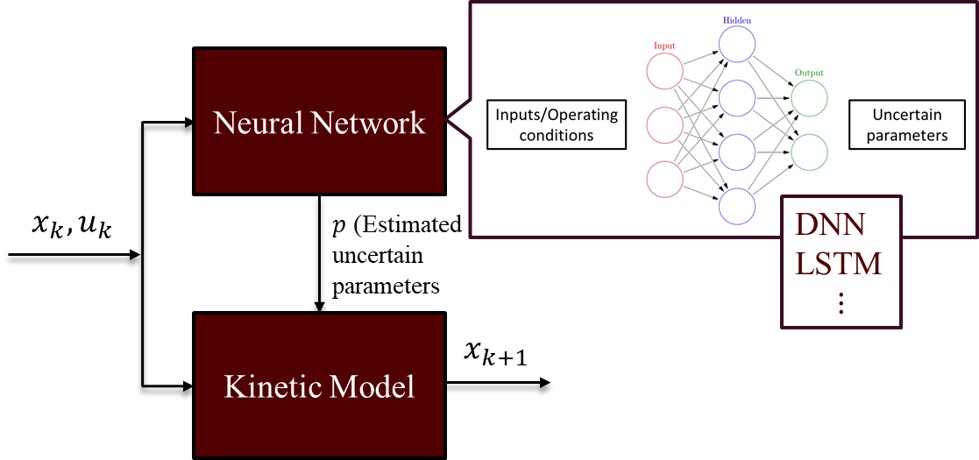
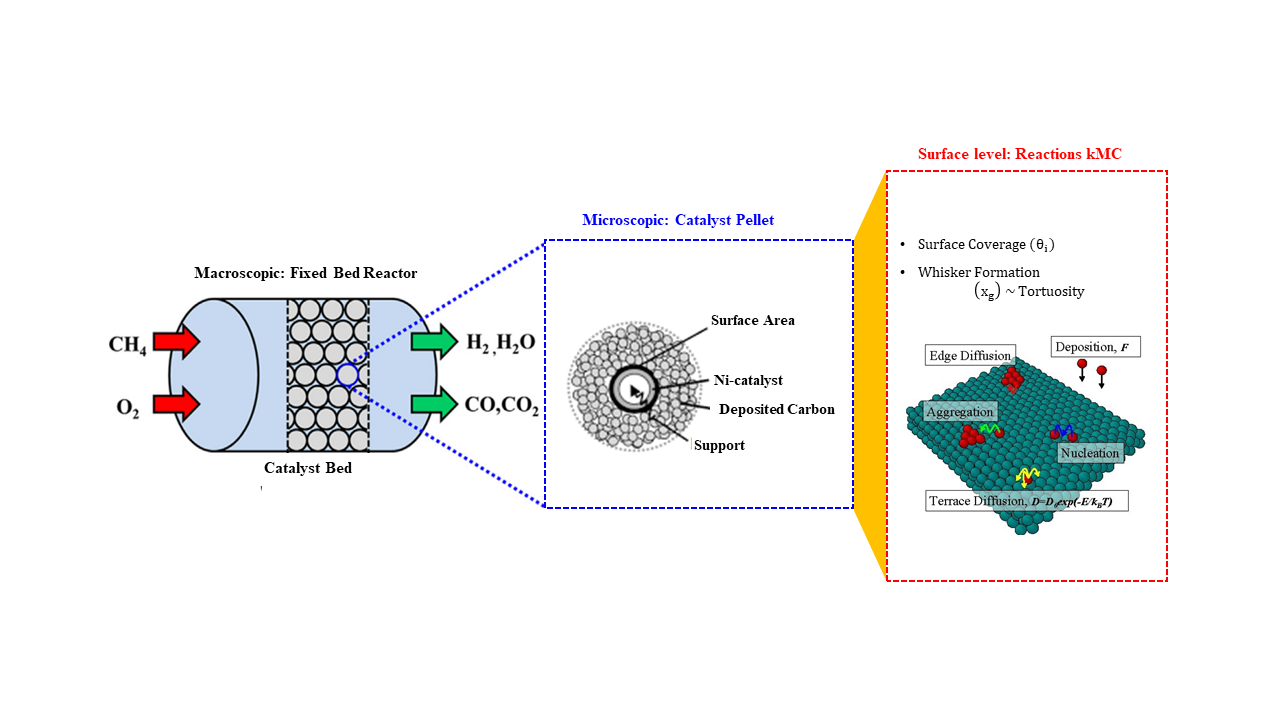
Kinetic Monte Carlo (KMC) is a widely employed technique for studying various phenomena such as transport, material properties, and chemical reactions, bridging the gap between the microscopic and macroscopic worlds. It serves as a crucial tool in understanding atomistic diffusion and catalysis. However, existing multiscale surface kinetic Monte Carlo simulation methods have limitations, leading to inconsistencies between theoretical and experimental findings. In our research, we aim to enhance these multiscale models by:

1) Developing frameworks that enable macroscopic computations over large space-time scales using microscopic simulations initialized at smaller scales

2) Distinguishing between “slow” and “fast” processes, treating the former stochastically at the KMC level and the latter deterministically

3) Introducing the concept of a super basin, representing a set of lattice configurations accessible through quasi-equilibrated processes.

Through these improvements, we seek to advance the accuracy and applicability of multiscale surface kinetic Monte Carlo simulations, fostering better agreement with experimental observations and theoretical investigations.

Kinetic modeling of fermentation processes is challenging due to complex micro-organism reactions and incomplete system knowledge. We have developed a hybrid modeling approach that combines kinetic and data-based models to improve accuracy and robustness. By integrating a deep neural network (DNN) with the kinetic model, we predict uncertain parameters and capture time-varying dependencies. The developed model is tested against an industrial-scale fermenter with a capacity of over 100,000 gallons. In the chemical industry, digital twins and optimal control algorithms are important for profitability. To overcome the challenges of limited sensors and infrequent measurements, we design a multi-rate state observer and a model predictive controller (MPC) for an industry-scale fermentation process to optimize input profiles and enhance productivity while considering process constraints.

Literature:

Shah, P., Sheriff, M. Z., Bangi, M. S. F., Kravaris, C., Kwon, J. S. I., Botre, C., & Hirota, J. (2023). Multi‐rate observer design and optimal control to maximize productivity of an industry‐scale fermentation process. AIChE Journal, 69(2), e17946.

Shah, P., Sheriff, M. Z., Bangi, M. S. F., Kravaris, C., Kwon, J. S. I., Botre, C., & Hirota, J. (2022). Deep neural network-based hybrid modeling and experimental validation for an industry-scale fermentation process: Identification of time-varying dependencies among parameters. Chemical Engineering Journal, 441, 135643.

Due to their highly desirable characteristics such as high energy density, less weight, and low self-discharge, Li-ion batteries are popularly deployed in various applications, including powering electric vehicles. With increasing operating cycles, the degradation in a battery significantly impacts its reliability and can lead to failure events. Often, the reliability of a battery is defined by its remaining useful life (RUL), temperature, and smoothness of applied voltage or current. Specifically, RUL, which can be estimated from the predicted battery degradation trend, provides an idea about the number of cycles remaining before a battery is expected to fail. An accurate RUL estimation aids in developing effective predictive maintenance strategies for enhancing the battery’s health. Though RUL estimation helps in predicting the long-term performance of a battery, it is essential to also predict the battery’s condition in the short term to better monitor its overall performance. This requires modeling the dynamics of other battery variables such as voltage and state of charge (SoC) that evolve with charge-discharge operation. Accurate prediction of SoC and voltage helps understand many critical battery characteristics such as available power, charging and discharging times, and temperature change. Additionally, undesired cases of over-charging and over-discharging can be effectively mitigated through SoC prediction. Thus, real-time assessment of these variables together with capacity degradation enables better management of a battery’s performance. Our group works on modeling and monitoring the performance of a battery by predicting the inter-cyclic and intra-cyclic battery dynamics and accurately estimating RUL to enhance the overall battery operational safety.

Literature:

Bhadriraju, F. Khan, and J. S. Kwon, “An adaptive data-driven approach for two-timescale dynamics prediction and remaining useful life estimation of Li-ion batteries”, Computers & Chemical Engineering, 2023.

 

Effective process control is crucial, both within and outside the training regions. Chemical processes can often undergo changes in their operating targets due to several factors, including modified product quality, new product design, business demands, and process economics. Such scenarios can require controlling the process at completely new operating conditions outside the training region of the existing model. However, data-driven models usually fail to extrapolate beyond their training domains, thus restricting their applicability only to their training regions. Developing another model for the new operating scenarios is not a trivial task due to the unavailability of historical process data. Because of this, implementing data-driven process control in new operating settings outside the training region remains a major challenge. Motivated by this challenge, developing a systematic approach to control a process outside the training region of its model is an interesting direction. Accordingly, the adaptation capabilities of OASIS together with a state estimator can be useful in effectively controlling a process in new operation domains.

Chemical processes are complex and often characterized by nonlinearity, time variation, and uncertainty. As a result, data-driven modeling approaches have gained widespread popularity in industry and academia for modeling these processes. However, a model trained offline is not sufficient to deal with process uncertainties, which are prevalent in chemical processes. This limitation necessitates an adaptive modeling approach that can predict nonlinear process dynamics in real-time by coping with process uncertainties. Based on this motivation, in our group, we work on developing data-driven adaptive modeling frameworks for modeling nonlinear process systems and predicting dynamics in real time. Specifically, we use the techniques of sparse regression with deep learning to build an adaptive sparse model that can readily cope with abrupt dynamical changes on-the-fly. Further, this developed model can be integrated into various process monitoring and control applications.

Literature:

Bhadriraju, M. S. F. Bangi, A. Narasingam, and J. S. Kwon, “Operable adaptive sparse identification of systems (OASIS): application to chemical processes”, AIChE J., 2020, 66, e16980.

Our research group is dedicated to the advancement of energy and polymer materials through innovative methods. Specifically, we employ a systematic integration of Density Functional Theory (DFT), Kinetic Monte Carlo (kMC), and data-driven Long Short-Term Memory (LSTM) techniques to investigate and analyze their properties. By adopting this multifaceted approach, our primary objective is to enhance our understanding of various materials, thereby paving the way for future breakthroughs in electrochemical catalysis, battery technology, and polymer systems.

Literature:

ACS Catal. 2022, 12, 24, 15609–15617 (DFT-kMC Analysis for Identifying Novel Bimetallic Electrocatalysts for Enhanced NRR Performance by Suppressing HER at Ambient Conditions Via Active-Site Separation)

ACS Catal. 2023, 13, XXX, 8336–8346 (Investigating High-performance Non-Precious Transition Metal Oxide Catalysts for Nitrogen Reduction Reaction: A Multifaceted DFT-kMC-LSTM Approach)

 

The traditional fault detection and diagnosis (FDD) methods employed for process monitoring follow a reactive fault management approach. These methods detect an already present fault and take corrective action to mitigate the damage to the process. In order to minimize the degradation that a fault can bring to a process, fault diagnosis methods aim at achieving early fault detection, which is still reactive fault management. By the time the fault has been detected and managed, the process might have been affected to some degree. This situation can be avoided by implementing fault prognosis approaches that predict the occurrence of an impending fault ahead of its time and take appropriate action beforehand. For fault prediction, it is essential to track the varying process dynamics in order to predict a fault in advance. For this purpose, employing an adaptive model such as OASIS that can readily cope with changing dynamics will aid in forecasting the future process behavior reasonably well, thereafter providing an early fault prediction.

Literature:

B. Bhadriraju, F. Khan, and J. S. Kwon, “OASIS-P: Operable adaptive sparse identification of systems for fault prognosis of chemical processes”, Journal of Process Control, 2021, 107, 114-126.

Our research group focuses on hybrid modeling, which combines physics-based models with data-driven techniques. While first-principles models capture process dynamics, they require significant resources and may struggle with complex mechanisms. Data-driven models are easy to construct but lack extrapolation and interpretability. We aim to develop efficient hybrid models that outperform machine learning-based models in terms of extrapolation and interpretation. Our approach involves using hybrid models to estimate unknown system dynamics in bio-fermentation. We develop first-principles models, conduct sensitivity analysis, and estimate time-varying parameters using neural networks. We have collaborated with multiple industrial partners and validated our models using data from lab-scale and industry-scale processes to ensure robustness. These hybrid models are integrated into a model predictive controller for optimal operation, enhancing productivity and cost efficiency while considering constraints. Our goal is to advance hybrid modeling, improve process understanding, and optimize chemical process operations through integration with state-of-the-art machine-learning approaches.

Literature:

Shah, M. Z. Sheriff, M. S. F. Bangi, C. Kravaris, J. S.-I. Kwon, C. Botre, and J. Hirota, “Deep neural network-based hybrid modeling and experimental validation for an industry-scale fermentation process: Identification of time-varying dependencies among parameters,” Chemical Engineering Journal, vol. 441, p. 135643, 2022.

Bangi, Mohammed Saad Faizan, and Joseph Sang-Il Kwon. “Deep hybrid modeling of a chemical process: Application to hydraulic fracturing.” Computers & Chemical Engineering 134 (2020): 106696.