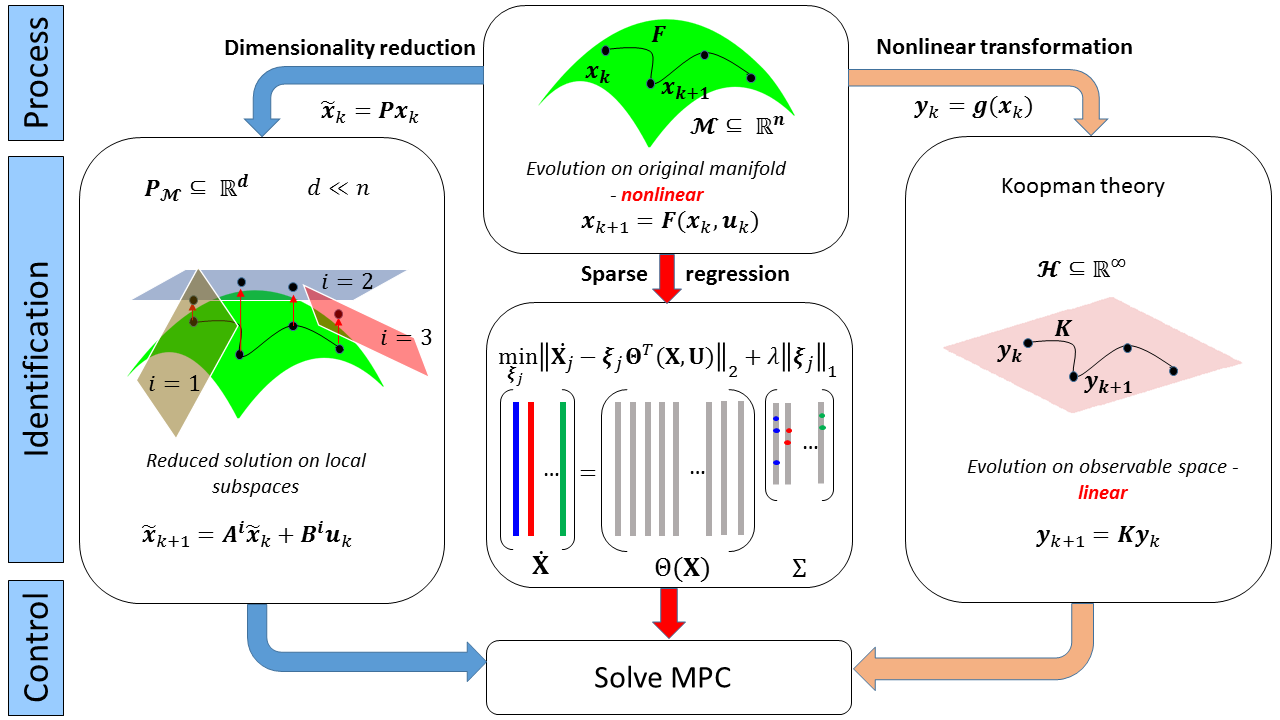
 Real life processes characterized by PDEs pose challenges when used in numerical simulations, due to high dimensionality and complexity. Approximate models aim to lower the complexity of such problems for use in process control. However, in many chemical and industrial processes these approximate models must be customized to accurately capture the dynamics over the entire state-space. In our group, we are developing a systematic framework to achieve accurate model identification and closed-loop control on three fronts: (i) by combining the concepts of domain partitioning and projection-based reduced order modeling, (ii) by leveraging machine learning tools such as sparse regression to discover interpretable models, and (iii) by adopting an operator-centric perspective of dynamical systems to develop linear models which enable the use of of simple linear control theory and results in standard convex optimal control problems. We further extend dimensionality reduction to the parameter space and integrate with a data assimilation technique for computationally tractable solutions to ill-posed inverse problems.
Real life processes characterized by PDEs pose challenges when used in numerical simulations, due to high dimensionality and complexity. Approximate models aim to lower the complexity of such problems for use in process control. However, in many chemical and industrial processes these approximate models must be customized to accurately capture the dynamics over the entire state-space. In our group, we are developing a systematic framework to achieve accurate model identification and closed-loop control on three fronts: (i) by combining the concepts of domain partitioning and projection-based reduced order modeling, (ii) by leveraging machine learning tools such as sparse regression to discover interpretable models, and (iii) by adopting an operator-centric perspective of dynamical systems to develop linear models which enable the use of of simple linear control theory and results in standard convex optimal control problems. We further extend dimensionality reduction to the parameter space and integrate with a data assimilation technique for computationally tractable solutions to ill-posed inverse problems.
Local model reduction
A. Narasingam and J. S. Kwon,” Development of local dynamic mode decomposition with control: Application to model predictive control of hydraulic fracturing,” Comp. & Chem. Eng., 2017, 106, 501-511. DOI: 10.1016/j.compchemeng.2017.07.002
A. Narasingam, P. Siddhamshetty and J. S. Kwon, “Temporal clustering for order reduction of nonlinear parabolic PDE systems with time-dependent spatial domains: Application to a hydraulic fracturing process,” AIChE J., 2017, 63, 3818-3831. DOI: 10.1002/aic.15733
Sparse identification of dynamics
A. Narasingam and J. S. Kwon, “Data-driven identification of interpretable reduced-order models using sparse regression,” Comp. & Chem. Eng., 2018, 119, 101-111. DOI: 10.1016/j.compchemeng.2018.08.010
S. Sidhu, A. Narasingam, P. Siddhamshetty and J. S. Kwon, “Model order reduction of nonlinear parabolic PDE systems with moving boundaries using sparse proper orthogonal decomposition: Application to hydraulic fracturing,” Comp. & Chem. Eng., 2018, 112, 92-100. DOI: 10.1016/j.compchemeng.2018.02.004
Koopman operator-based identification and control
A. Narasingam and J. S. Kwon, “Koopman Lyapunov-based model predictive control of nonlinear chemical process systems,” AIChE J DOI: 10.1002/aic.16743.